
The results of the pairwise tests appear below. Title "Pairwise comparison of independent ROC curves" These statements read the ROC statistics in the AUC data set and compute pairwise tests comparing the areas under the ROC curves. "AUC block 4" = "&auc4") / opaque position=bottomright

ROC CURVE IN SPSS 20 SERIES
Series x=_1mspec_ y=_sensit_ / group=block Lineparm x=0 y=0 slope=1 / transparency=.7 Yaxis values=(0 to 1 by 0.25) grid offsetmin=.05 offsetmax=.05

Xaxis values=(0 to 1 by 0.25) grid offsetmin=.05 offsetmax=.05 The ASPECT=1 option in the PROC SGPLOT statement creates a square plot as appropriate for an ROC plot which ranges from zero to one on both axes Note2. The PROC SQL step copies the AUC values into macro variables (AUC1-AUC4) to be used in PROC SGPLOT for display along with the ROC curves. The two DATA steps add the (0,0) points to the curves since these points are omitted in the OUTROC= data sets. These next statements create a comparative plot which overlays the ROC curves. The ROC statistics for the separate fits are shown below.
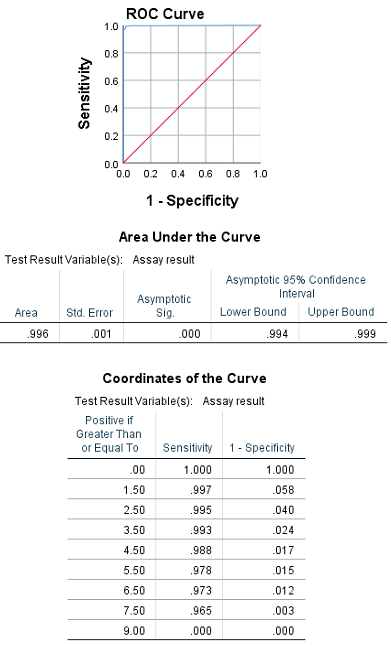
The ODS OUTPUT statement saves the ROC statistics in data set AUC. The OUTROC= option saves the ROC plot data in data set ROC. The ROCCI option plots the ROC curves and displays the estimated AUCs and their standard errors. In the following PROC LOGISTIC step, the BY statement requests that the specified model be separately fit to the data in each block. Input block entry lat lng n Y 14 1 1 8 2 1 16 1 2 9 1 The data give the number of damaged plants, Y, out of a total number of plants, n, in each of four blocks which are assumed to be independent. Researchers studied 16 varieties (entries) of wheat for their resistance to infestation by the Hessian fly. The following uses the data in the example titled "Binomial Counts in Randomized Blocks" in the GLIMMIX documentation. See this note for an example of that situation. A similar case is comparing the performance of a single model that is fit to one data set and then used to score several other independent samples. The following example illustrates plotting and comparing independent ROC curves from models that are separately fitted to independent samples. Specify the ROCCI option Note1 in the MODEL statement in PROC LOGISTIC to display the areas and standard errors needed to compute the above statistic. A p-value can be obtained using the PROBCHI function in the DATA step. The statistic, ChiSq, is distributed as chi-square with one degree of freedom. Where AUC 1 and AUC 2 are the areas under the two independent ROC curves, and s 1 and s 2 are their respective standard errors. Gönen (2007) presents the following large-sample test to compare the areas under two independent ROC curves:ĬhiSq = ( AUC 1 - AUC 2) 2 / ( s 1 2 + s 2 2) , For an example of comparing dependent ROC curves, see "Comparing Receiver Operating Characteristic Curves" in the Examples section of the LOGISTIC documentation. Those statements compare dependent curves, such as when comparing competing models fit to the same set of observations. ROC curves from models fit to two or more independent groups of observations are not dependent and therefore cannot be compared using the ROC and ROCCONTRAST statements in PROC LOGISTIC.


 0 kommentar(er)
0 kommentar(er)
